 En Las Leyes, 757b/d, Platón analiza «dos clases de igualdad». «Una de ellas… es la igualdad de medida, peso o número (es decir, igualdad numérica o aritmética); pero la verdadera y la mejor igualdad… es la que distribuye más a los mayores y menos a los más pequeños, dando a cada uno la medida debida, de acuerdo con la naturaleza… Al concederle mayores honores a quienes son superiores por sus virtudes, y menores a quienes son inferiores en virtud y origen, distribuye a cada uno lo apropiado, de acuerdo con este principio de las proporciones (racionales). y es esto precisamente lo que llamaremos «justicia política». Y quienquiera que funde un Estado hará de éste el único objetivo de su legislación… A saber, esta justicia que, como decimos, es la igualdad natural y que se distribuye según lo requiere la situación entre los desiguales». La segunda de estas dos igualdades, que constituye lo que Platón llama «justicia política» (y lo que Aristóteles denomina «justicia distributiva») y que Platón describe (y también Aristóteles) como «igualdad proporcional» —la mejor, la más verdadera y natural de las igualdades— recibió posteriormente el nombre de «geométrica» […] en oposición a la
En Las Leyes, 757b/d, Platón analiza «dos clases de igualdad». «Una de ellas… es la igualdad de medida, peso o número (es decir, igualdad numérica o aritmética); pero la verdadera y la mejor igualdad… es la que distribuye más a los mayores y menos a los más pequeños, dando a cada uno la medida debida, de acuerdo con la naturaleza… Al concederle mayores honores a quienes son superiores por sus virtudes, y menores a quienes son inferiores en virtud y origen, distribuye a cada uno lo apropiado, de acuerdo con este principio de las proporciones (racionales). y es esto precisamente lo que llamaremos «justicia política». Y quienquiera que funde un Estado hará de éste el único objetivo de su legislación… A saber, esta justicia que, como decimos, es la igualdad natural y que se distribuye según lo requiere la situación entre los desiguales». La segunda de estas dos igualdades, que constituye lo que Platón llama «justicia política» (y lo que Aristóteles denomina «justicia distributiva») y que Platón describe (y también Aristóteles) como «igualdad proporcional» —la mejor, la más verdadera y natural de las igualdades— recibió posteriormente el nombre de «geométrica» […] en oposición a la
primera, esto es, la igualdad inferior y democrática que se llamó «aritmética». […]
De acuerdo con la tradición […], sobre la puerta de la Academia de Platón se veía la siguiente leyenda: «¡El que no sepa geometría que no entre en esta casa!», Sospecho que esta inscripción no quiere poner el acento tan sólo en la importancia de los estudios matemáticos, sino que también significa lo siguiente: «La aritmética (o, mejor dicho, la teoría pitagórica del número) no es suficiente; también debéis conocer la geometría». A continuación trataré de explicar las razones que tengo para creer que esta última frase resume correctamente una de las más importantes contribuciones de Platón a la ciencia helénica. […]
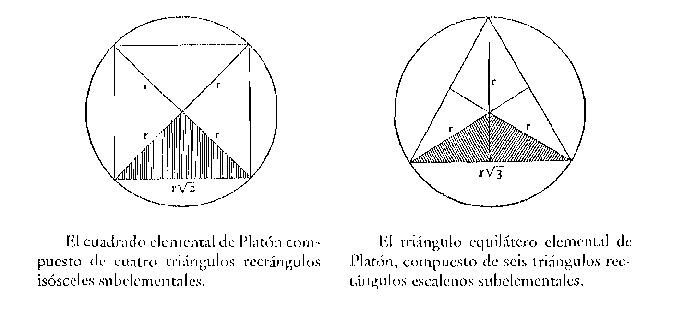
(3) En el Timeo, Platón necesita para la construcción de los Cuerpos Primarios un Cuadrado Elemental y un Triángulo Equilátero Elemental. Estas dos Figuras se hallan compuestas, a su vez, de dos tipos diferentes de triángulos subelementales, a saber, el equivalente a la mitad de un cuadrado que introduce la √2 y el equivalente a la mitad de un triángulo equilátero que introduce la √3. […]
Y bien, no puede caber ninguna duda de que existe una referencia a cierta conjetura no probada en el mismo pasaje del Timeo en que Platón se refiere a la razón que tuvo para elegir sus triángulos subelementales, pues expresa (Timeo, 53c/d): «Todos los triángulos derivan de dos, cada uno de los cuales tiene un ángulo recto…; de estos triángulos, uno (la mitad de un cuadrado) tiene a cada lado la mitad de un ángulo recto … y lados iguales; el otro (el escaleno)… tiene lados desiguales. Supondremos que estos dos constituyen los principios primordiales… de acuerdo con una explicación que combina la probabilidad (o la conjetura probable) con la necesidad (la prueba). Principios como éste y aun otros más remotos todavía, son conocidos por el cielo y por aquellos hombres a quienes aquél ha favorecido». […]
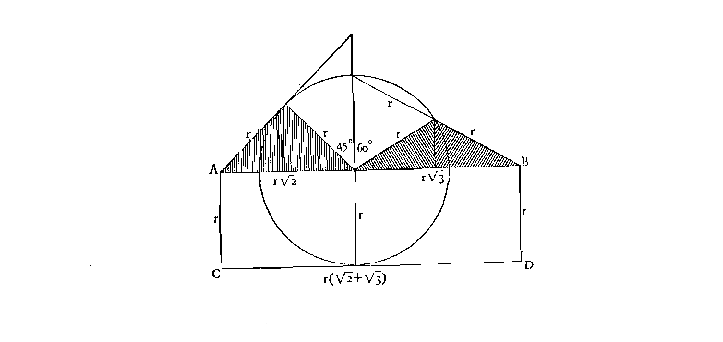
Quizá pueda deducirse una razón adicional para nuestra interpretación —razón de la cual no hay datos ciertos en el texto platónico— de la siguiente consideración: es un hecho curioso que √2 +√3 se aproxime estrechamente al valor de π. […] Existen, pues, dos modos por los cuales Platón podría haber descubierto la ecuación √2 +√3 = π y el segundo parece casi ineludible. Resulta plausible entonces que Platón conociera esta ecuación pero ignorando si se trataba de una igualdad exacta o tan sólo de una aproximación. Pero siendo esto así, quizá podamos responder a la «segunda pregunta» mencionada más arriba, en (3), es decir, por qué Platón compuso su cuadrado elemental de cuatro triángulos subelementales (mitades del cuadrado) en lugar de dos, y su triángulo equilátero elemental de seis triángulos subelementales (mitades de equilátero), en lugar de dos. Si examinamos las dos primeras figuras que reproducimos a continuación, veremos que la construcción da realce al centro de los círculos circunscritos e inscritos y, en ambos casos, a los radios del círculo circunscrito. (En el caso del triángulo equilátero, también aparece el radio del círculo inscrito, pero parecería que Platón hubiera estado pensando en el círculo circunscrito, puesto que lo menciona explícitamente en su descripción del método de composición del triángulo equilátero con el nombre de «diagonal», véase el Timeo, 54d/e; véase, asimismo, 54b).
Si ahora trazamos estos dos círculos circunscritos o, más específicamente, si inscribimos el cuadrado y el triángulo equilátero elementales en un círculo de radio r, hallaremos que la suma de los lados de estas dos figuras se aproxima a rπ; en otras palabras, la construcción de Platón sugiere una de las soluciones aproximadas más simples de la cuadratura del círculo, como lo demuestran nuestras tres figuras. En vista de todo esto, bien podría suceder que la conjetura de Platón y su ofrecimiento de «un premio con toda nuestra buena voluntad» —de que hablamos en (3)— se hubieran referido no sólo al problema general de la conmensurabilidad de los irracionales, sino también al problema especial de si a partir de √2 +√3 se puede llegar o no a la cuadratura del círculo.
Popper, Karl (2006). La sociedad abierta y sus enemigos. Barcelona: Paidós, 561-2, 564-7.
revistametabasis.com
ISSN 2605-3489
 Badiou opta por la definición de los números reales según el método de cortaduras de Dedekind y estudia el teorema fundamental de la ontología del número, el teorema de existencia de un número único a partir de la reflexión de Dedekind sobre el concepto de continuidad, que establece una comparación entre los números racionales y los puntos de la recta L. Evidentemente existe una infinidad de puntos que no corresponden a ningún número racional. La cuestión que se plantea es, por lo tanto, cómo se introducen los números irracionales para que el campo de los números adquiera la misma compleción (continuidad) que la línea recta.
Badiou opta por la definición de los números reales según el método de cortaduras de Dedekind y estudia el teorema fundamental de la ontología del número, el teorema de existencia de un número único a partir de la reflexión de Dedekind sobre el concepto de continuidad, que establece una comparación entre los números racionales y los puntos de la recta L. Evidentemente existe una infinidad de puntos que no corresponden a ningún número racional. La cuestión que se plantea es, por lo tanto, cómo se introducen los números irracionales para que el campo de los números adquiera la misma compleción (continuidad) que la línea recta. Más aún, lo que está vedado en el campo político, desborda en el campo religioso. Del psicoanálisis aprendimos que todo lo reprimido retorna de una forma u otra, y esto es ineludible. La religión se convirtió en la válvula de escape de la sociedad palestina, y toda la furia y humillación reprimida se vuelca en la mezquita. El Corán es el contradiscurso estatal, y la actividad religiosa es lo más cercano a lo que J. Habermas define como un «contraproyecto al mundo jerárquico de dominación». Así como el proletario desarrolla un saber propio destinado a usurpar el poder del patrón, el palestino desarrolla una conducta de orden religioso destinada a liberarse del dominio israelí. En esta área Israel no ha logrado infiltrase lo suficiente para reprimir el espíritu rebelde de la religión, y a través de ella dirigen su ofensiva, mantienen su identidad, rescatan algo de su dignidad y canalizan su malestar nacional.
Más aún, lo que está vedado en el campo político, desborda en el campo religioso. Del psicoanálisis aprendimos que todo lo reprimido retorna de una forma u otra, y esto es ineludible. La religión se convirtió en la válvula de escape de la sociedad palestina, y toda la furia y humillación reprimida se vuelca en la mezquita. El Corán es el contradiscurso estatal, y la actividad religiosa es lo más cercano a lo que J. Habermas define como un «contraproyecto al mundo jerárquico de dominación». Así como el proletario desarrolla un saber propio destinado a usurpar el poder del patrón, el palestino desarrolla una conducta de orden religioso destinada a liberarse del dominio israelí. En esta área Israel no ha logrado infiltrase lo suficiente para reprimir el espíritu rebelde de la religión, y a través de ella dirigen su ofensiva, mantienen su identidad, rescatan algo de su dignidad y canalizan su malestar nacional.
 El 25 de diciembre fue instituido como fecha del nacimiento de Jesucristo, como el día de la Natividad de Cristo, y reconocido en Constantinopla el año 379 como fecha de significado sobrenatural —el nacimiento del Niño Dios— emanada del depósito de la fe y tan sobrenatural como lo había sido la fecha de la concepción inmaculada. Sin embargo esta fecha, sin duda estrictamente religiosa, estaba involucrada con un acontecimiento natural, como podría serlo el día del solsticio de invierno, en realidad la noche más larga del año. Es cierto que esta fecha natural, a saber, la del solsticio de invierno, había sido ya involucrada en instituciones culturales muy afines a la religión en el calendario y, más aún, en la institución del Dies natalis Solis invicti, que el emperador Aureliano estableció en conmemoración de su victoria sobre Palmira el día 25 de diciembre del año 274.
El 25 de diciembre fue instituido como fecha del nacimiento de Jesucristo, como el día de la Natividad de Cristo, y reconocido en Constantinopla el año 379 como fecha de significado sobrenatural —el nacimiento del Niño Dios— emanada del depósito de la fe y tan sobrenatural como lo había sido la fecha de la concepción inmaculada. Sin embargo esta fecha, sin duda estrictamente religiosa, estaba involucrada con un acontecimiento natural, como podría serlo el día del solsticio de invierno, en realidad la noche más larga del año. Es cierto que esta fecha natural, a saber, la del solsticio de invierno, había sido ya involucrada en instituciones culturales muy afines a la religión en el calendario y, más aún, en la institución del Dies natalis Solis invicti, que el emperador Aureliano estableció en conmemoración de su victoria sobre Palmira el día 25 de diciembre del año 274. En Las Leyes, 757b/d, Platón analiza «dos clases de igualdad». «Una de ellas… es la igualdad de medida, peso o número (es decir, igualdad numérica o aritmética); pero la verdadera y la mejor igualdad… es la que distribuye más a los mayores y menos a los más pequeños, dando a cada uno la medida debida, de acuerdo con la naturaleza… Al concederle mayores honores a quienes son superiores por sus virtudes, y menores a quienes son inferiores en virtud y origen, distribuye a cada uno lo apropiado, de acuerdo con este principio de las proporciones (racionales). y es esto precisamente lo que llamaremos «justicia política». Y quienquiera que funde un Estado hará de éste el único objetivo de su legislación… A saber, esta justicia que, como decimos, es la igualdad natural y que se distribuye según lo requiere la situación entre los desiguales». La segunda de estas dos igualdades, que constituye lo que Platón llama «justicia política» (y lo que Aristóteles denomina «justicia distributiva») y que Platón describe (y también Aristóteles) como «igualdad proporcional» —la mejor, la más verdadera y natural de las igualdades— recibió posteriormente el nombre de «geométrica» […] en oposición a la
En Las Leyes, 757b/d, Platón analiza «dos clases de igualdad». «Una de ellas… es la igualdad de medida, peso o número (es decir, igualdad numérica o aritmética); pero la verdadera y la mejor igualdad… es la que distribuye más a los mayores y menos a los más pequeños, dando a cada uno la medida debida, de acuerdo con la naturaleza… Al concederle mayores honores a quienes son superiores por sus virtudes, y menores a quienes son inferiores en virtud y origen, distribuye a cada uno lo apropiado, de acuerdo con este principio de las proporciones (racionales). y es esto precisamente lo que llamaremos «justicia política». Y quienquiera que funde un Estado hará de éste el único objetivo de su legislación… A saber, esta justicia que, como decimos, es la igualdad natural y que se distribuye según lo requiere la situación entre los desiguales». La segunda de estas dos igualdades, que constituye lo que Platón llama «justicia política» (y lo que Aristóteles denomina «justicia distributiva») y que Platón describe (y también Aristóteles) como «igualdad proporcional» —la mejor, la más verdadera y natural de las igualdades— recibió posteriormente el nombre de «geométrica» […] en oposición a la
 El elemento constitutivo de acción intencional del ideograma se manifiesta aun más nítidamente en el papel que tiene en la demostración geométrica. Se ha querido que la figura que acompaña al texto de una demostración posea un valor heurístico no esencial a la misma. Y sí es esencial: el ideograma, en este caso la figura […], es imprescindible para la elaboración y no sólo comprensión de la demostración geométrica. La figura geométrica no es mera ilustración de un texto escrito en lenguaje natural, sino que implica lo no explicitado en el enunciado y supone una construcción espacial —no sólo lineal— que culmina en la superposición final, totalizadora de la demostración del teorema. No es, en modo alguno, prolongación serializada del texto o discurso fonológico escrito.
El elemento constitutivo de acción intencional del ideograma se manifiesta aun más nítidamente en el papel que tiene en la demostración geométrica. Se ha querido que la figura que acompaña al texto de una demostración posea un valor heurístico no esencial a la misma. Y sí es esencial: el ideograma, en este caso la figura […], es imprescindible para la elaboración y no sólo comprensión de la demostración geométrica. La figura geométrica no es mera ilustración de un texto escrito en lenguaje natural, sino que implica lo no explicitado en el enunciado y supone una construcción espacial —no sólo lineal— que culmina en la superposición final, totalizadora de la demostración del teorema. No es, en modo alguno, prolongación serializada del texto o discurso fonológico escrito.
 obra de forma dispersa, y así permanece todavía hoy, siendo buena parte de ella inencontable: pese a haber publicado numerosas obras en editoriales de prestigio, especialmente en el período que abarca desde 1996 (año de publicación de El mito de la cultura) hasta el año 2010 (publicación de El fundamentalismo democrático), estas ediciones, por el propio proceso de oferta y demanda, pronto fueron descatalogadas y se convirtieron a día de hoy en prácticamente inencontrables.
obra de forma dispersa, y así permanece todavía hoy, siendo buena parte de ella inencontable: pese a haber publicado numerosas obras en editoriales de prestigio, especialmente en el período que abarca desde 1996 (año de publicación de El mito de la cultura) hasta el año 2010 (publicación de El fundamentalismo democrático), estas ediciones, por el propio proceso de oferta y demanda, pronto fueron descatalogadas y se convirtieron a día de hoy en prácticamente inencontrables. entíficas como la Geometría y la Aritmética), que no permite hablar, sin ir más lejos, de una ciencia unificada. Esta idea del desbordamiento del género ha hecho especial fortuna en Lingüística y Retórica; así, Quintiliano en sus Instituciones Retóricas señala la metábasis como un recurso estilístico consistente en la sustantivación de un adjetivo (por ejemplo, en la frase «Los valientes avanzaron»), que irá convirtiendo progresivamente lo que con Aristóteles fue una caracterización de cosas, en una caracterización meramente semántica, de palabras.
entíficas como la Geometría y la Aritmética), que no permite hablar, sin ir más lejos, de una ciencia unificada. Esta idea del desbordamiento del género ha hecho especial fortuna en Lingüística y Retórica; así, Quintiliano en sus Instituciones Retóricas señala la metábasis como un recurso estilístico consistente en la sustantivación de un adjetivo (por ejemplo, en la frase «Los valientes avanzaron»), que irá convirtiendo progresivamente lo que con Aristóteles fue una caracterización de cosas, en una caracterización meramente semántica, de palabras. La filosofía, y sobre todo, en su forma sistemática, no brota de la ignorancia sino de saberes efectivos de primer grado, y por ello la filosofía puede considerarse como un saber de segundo grado. Frente a las distinciones un tanto artificiosas entre una tradición «analítica», centrada en la ciencia, y una tradición «continental», centrada en el análisis de los textos de la tradición, el materialismo filosófico clasifica ambas como una filosofía «centrada» en el análisis de las ciencias, en primer lugar, y una filosofía «exenta» de los problemas del presente, realizada por profesores y para profesores, en el segundo caso.
La filosofía, y sobre todo, en su forma sistemática, no brota de la ignorancia sino de saberes efectivos de primer grado, y por ello la filosofía puede considerarse como un saber de segundo grado. Frente a las distinciones un tanto artificiosas entre una tradición «analítica», centrada en la ciencia, y una tradición «continental», centrada en el análisis de los textos de la tradición, el materialismo filosófico clasifica ambas como una filosofía «centrada» en el análisis de las ciencias, en primer lugar, y una filosofía «exenta» de los problemas del presente, realizada por profesores y para profesores, en el segundo caso. El modo de la «incorporación» en una categoría dada de contenidos propios de otras categorías o campos, de suerte que una tal incorporación de lugar a contextos determinados nuevos. El término «incorporación» se toma aquí en sentido muy amplio; en todo caso, no se reduce al concepto de «involucración entre categorías», que tiene un alcance más preciso (por ejemplo: hablamos de «involucración de la Biología y de la Cristalografía» en situaciones, gnoseológicamente relevantes, tales como las constituidas por la presencia de cristales no orgánicos de calcita en la especie Paracentrotus lividus, que obligan a confrontar las categorías cristalográficas y las biológicas; o bien, hablamos de «involucración de la Aritmética y de la Geometría» en situaciones gnoseológicas relevantes tales como la constituida por la «relación de Leibniz»: 1/1 – 1/3 + 1/5 – 1/7… →π/4, que obliga a comunicar los géneros matemáticos, tradicionalmente designados como cantidad discreta y como cantidad continua, considerados como incomunicables).
El modo de la «incorporación» en una categoría dada de contenidos propios de otras categorías o campos, de suerte que una tal incorporación de lugar a contextos determinados nuevos. El término «incorporación» se toma aquí en sentido muy amplio; en todo caso, no se reduce al concepto de «involucración entre categorías», que tiene un alcance más preciso (por ejemplo: hablamos de «involucración de la Biología y de la Cristalografía» en situaciones, gnoseológicamente relevantes, tales como las constituidas por la presencia de cristales no orgánicos de calcita en la especie Paracentrotus lividus, que obligan a confrontar las categorías cristalográficas y las biológicas; o bien, hablamos de «involucración de la Aritmética y de la Geometría» en situaciones gnoseológicas relevantes tales como la constituida por la «relación de Leibniz»: 1/1 – 1/3 + 1/5 – 1/7… →π/4, que obliga a comunicar los géneros matemáticos, tradicionalmente designados como cantidad discreta y como cantidad continua, considerados como incomunicables). Las técnicas y la filosofía no tienen un desarrollo esencial común, ni pertenecen al mismo género ni a la misma especie. Cabe inclinarse por encontrar algo propio a ambas, sin ser estrictamente suyo. A este conjunto en que cabe incluirlas lo llamamos «propiedad destructiva»: Prometeo destructor. Tanto histórica como operativamente las técnicas comienzan por golpear, romper, triturar, rasgar, trocear, partir, dividir, separar lo que tienen entre manos. Del mismo modo comenzó la filosofía y del mismo modo opera, critica, desmonta, clasifica, diferencia, distingue. Son modos a escalas distintas del des-hacer. Si la técnica destruye morfologías naturales, la filosofía será el modo de destruir nematologías, mitos, ideas metafísicas y cosmovisiones a las que se enfrenta permanentemente.
Las técnicas y la filosofía no tienen un desarrollo esencial común, ni pertenecen al mismo género ni a la misma especie. Cabe inclinarse por encontrar algo propio a ambas, sin ser estrictamente suyo. A este conjunto en que cabe incluirlas lo llamamos «propiedad destructiva»: Prometeo destructor. Tanto histórica como operativamente las técnicas comienzan por golpear, romper, triturar, rasgar, trocear, partir, dividir, separar lo que tienen entre manos. Del mismo modo comenzó la filosofía y del mismo modo opera, critica, desmonta, clasifica, diferencia, distingue. Son modos a escalas distintas del des-hacer. Si la técnica destruye morfologías naturales, la filosofía será el modo de destruir nematologías, mitos, ideas metafísicas y cosmovisiones a las que se enfrenta permanentemente.