Las cosas como son
Reconozco que me siento incómodo al escribir esta columna. Hubiera preferido no escribirla. Incluso, me ha costado varios días ponerme a teclear ante la pantalla.
Me refiero a un reportaje que firmó David Orihuela y que salió publicado en La Nueva España el 5 de Noviembre próximo pasado. En ese reportaje se relacionaba a Gustavo Bueno Martínez con un partido político. Incluso salía un testimonio de un familiar suyo sobre esa relación.
Desde que conocí a Gustavo Bueno hace bastantes años, no me he sentido tan a disgusto. Creo que uno de los peores favores que alguien puede hacer a un filósofo es ligarlo con un partido, sea el que sea. No me refiero a un filósofo cualquiera sino a alguien como Gustavo Bueno.
El precedente de Elisabeth Nietzsche
Inmediatamente recordé la película Lou Andreas Salomé, de 2016, donde hacia el minuto 50, podemos ver una escena que viene al caso. Un joven biógrafo de Lou viene a enseñarle un libro. Quiere mostrarle un libro de Elisabeth Nietzsche, la hermana del filósofo. “Ha escrito este libro que está lleno de falsedades sobre usted”. Lou no quiere mirar el libro. “Ya sé sus historias sobre mí. Creo que es mucho peor falsear la obra de Nietzsche con la intención de otorgar al nacional-socialismo cierta aureola pseudofilosófica”.
Lou Andreas Salomé fue una mujer muy original, no solo en su forma de vivir sino en lo que hizo esta examiga del filósofo y examante del poeta Rainer María Rilke. Escribió varios libros interesantes y contribuyó a la teoría del narcisismo de los psicoanalistas. Murió en 1937.
¿Qué ocurrió después de la muerte de Elisabeth Nietzsche? Que, en medio de los obstáculos que Elisabeth Nietzsche había creado, el valor de la filosofía de su hermano volvió a salir a flote y, sobre todo, que cualquiera puede consultar las obras completas del filósofo alemán.
Vayamos a las cosas mismas. El “experimento Kuleshov”.
Quiero contar lo que he venido haciendo durante algunos días, después de leer el reportaje citado sobre Bueno. Seguí el mismo proceder que Sherlock Holmes, el Padre Brown, el Doctor House y Grissom, de la serie CSI. ¿En qué consiste su manera de trabajar? En que no creen en las palabras sino en las pruebas. Entonces, consulté la Bibliografía de Gustavo Bueno, ordenada cronológicamente, y que cualquier interesado puede encontrar en la Página Web de la Fundación Gustavo Bueno. Pues bien, no he encontrado, en los escritos de Bueno de la última década, ni la más ligera mención sobre ese partido.
En el diario digital El Español, sí he encontrado una foto de Bueno junto al político de ese partido que aparece en el reportaje de La Nueva España. Es la fotografía tópica de alguien presentando a un conferenciante en una Escuela de Verano. ¿Y solo existe esa prueba, aparte de las declaraciones del familiar?
Pues entonces nos encontramos ante un nuevo caso del experimento Kuleshov. Por si alguien que lea esta columna quiere comprobar lo que voy a escribir, puede ir a algo tan familiar como la Wikipedia. En 1922, el célebre director soviético Vsévolod Pudovkin describió un supuesto experimento que realizó junto con Lev Kuleshov en el cual explicaba lo que llamó “el efecto Kuleshov”. ¿En qué consistió el experimento? En seleccionar unos primeros planos del rostro neutral del conocido actor Iván Mozzhujin. A continuación, pusieron al lado un plato de sopa. ¿Resultado? Quienes veían las dos imágenes, deducían que el actor parecía mirar al plato. En la segunda, el actor aparecía junto a la toma de una mujer en un ataúd. No es muy complicado deducir lo que interpretaban quienes veían el conjunto: El actor estaba triste. Finalmente, ponían la toma de una niña jugando con un osito de peluche. En los tres casos, la cara era la misma. Kuleshov creó un sintagma pretencioso – «geografía creativa»- pero lo importante era que se interesó por los efectos que producía el montaje.
La cara neutra de Bueno
Adelanto ya que Bueno, un prodigio de expresión cuando hablaba, mostraba una cara más neutra todavía que la de Mozzhujin cuando le alababan al presentarlo en una conferencia. Y eso que a Bueno le alabaron mucho. Pero muchísimo. Pues él, imperturbable. No mostraba la autocomplacencia de haber nacido y haberse conocido.
Pues bien, pongamos a Bueno sentado junto a su íntimo amigo José María Laso, el comunista más consecuente que muchos hemos conocido. ¿Quería esto decir que Bueno era comunista, en la línea de alguien que convirtió sus años de cárcel en una pasión por el saber y en vivir de acuerdo con sus ideas?
O pongamos a Bueno sentado junto a Agustín García Metola, alcalde socialista durante años y años de Santo Domingo de la Calzada. ¿Quiere esto decir que Bueno era socialista como el, a mi parecer, muy simpático alcalde?
¿Qué quiere decir que Bueno aparezca sentado junto a un político español en ciernes? ¿Qué Bueno bendice ese partido?
Quien piense así es un apasionado por subir al Monte Camelo (sin erre, por supuesto).
Es que da risa todo este asunto.
Los enemigos de Bueno, “verdura de las eras”
Gustavo Bueno fue, durante años, el filósofo más solicitado desde muchos ámbitos e independiente de la orientación partidista. Recuerdo que un historiador de izquierdas, colega muy trabajador y muy gracioso, me contó que estaba organizando un Congreso de Historia y que, para inaugurar las sesiones, iba a invitar a Gustavo Bueno porque “llena los salones”. Los periodistas le buscaban para entrevistarlo. Bueno siempre proporcionaba titulares, después de haber impartido una conferencia, claro está, no en lugar de la conferencia. Primero, los conceptos y las ideas. Después, y como Bueno tenía un sentido del humor como pocos, hablaba para un público mucho más amplio.
También es verdad que tenía una debilidad que, realmente, era una fortaleza: No aguantaba las tonterías. Y se indignaba, desinhibido, ridiculizando al que había dicho algunas bobadas. Como he repetido varias veces, a Bueno le sobraban enemigos sin importancia y le faltaban auténticos contrincantes. Algunos me han hecho ver que las declaraciones del familiar habían dado alas a los enemigos de Bueno. Por ese lado, les he respondido, no hay problema alguno. Tienen mala baba, pero les faltan conceptos. Como escribiría Jorge Manrique, son como “verdura de las eras”.
Bueno no era una persona recortadita con tijeras, como algunas figuras con las que se entretienen los que tienen pocos años. Leyéndolo, los inteligentes desbordan los límites y rompen las costuras. Como les ocurre a quienes conocen, leen y estudian a los autores geniales.
Conviene rebobinar los recuerdos que tenemos de la vida de Gustavo Bueno diez años antes de su muerte: Renunció a viajes y conferencias y se dedicó a cuidar de su mujer, Carmen. Y solo la sobrevivió dos días. Entonces, ¿a qué dedicó su tiempo? A escribir y publicar, a grabar en vídeo las sesiones que mantenía en su Fundación. Impresiona ver la gran creatividad de este filósofo hasta su muerte. Podemos decir que murió con las botas puestas.
Entonces, ¿qué?
Ya lo escribí en La Nueva España, en Agosto, con motivo del segundo aniversario de su muerte: El gran atractor de quienes han estudiado y se han entusiasmado con Bueno en algún momento de su vida, es publicar sus Obras Completas. ¿Que los responsables de sus derechos se deciden por una versión digital? Muy bien. Hay precedentes de un escritor tan prolífico como Chesterton.
El familiar que hizo esas declaraciones tan desafortunadas puede enmendar su yerro. Domina muy bien el mundo digital. Como muy pocos en España y más allá. Lo único que necesita es centrarse en su padre y en su obra. Si se desvía de esa meta, garantizo que acabará metiendo todavía más la pata.
Otros muchos quizá prefieran, quiero decir, prefiramos, que lo mejor es contar con una versión impresa de esas obras. Como decía Oscar Wilde del matrimonio, “reúne el máximo de tentación y el máximo de oportunidad”. Efectivamente, la edición cada vez es más barata y no hace falta una gran inversión. Lo importante y, a la vez, urgente, es saber citar a Bueno en cualquier artículo, trabajos finales de Grado y Master, Tesis Doctorales, libros… ¿Hay desafío más documentalmente atractivo que crear un problema de espacio a las Bibliotecas para que puedan acoger las voluminosas Obras Completas de Gustavo Bueno Martínez?
Y finalmente, pienso que una tarea muy importante es dar con un autor como Harold Raley. ¿Quién es este autor? Un norteamericano que se entusiasmó con la filosofía de Julián Marías y logó hacer comprensible, y en un lenguaje sencillo, la filosofía de Julián Marías. En 1977, la Editorial Austral publicó La visión responsable. La filosofía de Julián Marías. ¡Qué gran libro! Gustavo Bueno es un filósofo mucho más importante que Julián Marías. Sin embargo, Bueno aún no dispone de un estudio que resuma muy bien su filosofía. Es en lo único en que, a mi entender, Marías supera a Bueno. ¿Para cuándo van a cambiar las cosas?
Valbuena, Felicísimo (02 de Diciembre de 2018). La filosofía de Gustavo Bueno está por encima de su familia y más allá de los partidos políticos, La Nueva España, 34.35.
ISSN 2605-3489
Pues para las criaturas divinas existe un período comprendido por un número perfecto; y para las humanas, otro número, que es el primero en que, habiendo recibido tres distancias y cuatro límites los incrementos dominantes y dominados de lo que iguala y desiguala y acrece y aminora, estos incrementos hacen aparecer todas las cosas como acordadas y racionales entre sí. De aquello, la base epítrita, acoplada con la péntada y tres veces acrecida, proporciona dos armonías: la una, igual en todas sus partes, siendo éstas varias veces mayores que cien; y la otra, equilátera en un sentido, pero oblonga, comprende cien números de la diagonal racional de la péntada, disminuido cada uno en una unidad, o de la irracional, disminuidos en dos, y cien cubos de la tríada. He aquí el número geométrico que de tal modo impera todo él sobre los mejores o peores nacimientos.
s, perfectos y amigos, ¿qué les impide comprometerse en matrimonio? Lo hacen. Son o, mejor, se denomina número nupcial al que posee esta particularidad:
El número nupcial viene a ser la prolongación del teorema de Pitágoras sobre el cuadrado de la hipotenusa, pero adaptado a tres dimensiones (cubos) y para longitudes proporcionales a 3, 4, 5 y 6. Viene a decir que la suma de los cubos construidos sobre los tres lados de un triángulo rectángulo de lados proporcionales a 3, 4, 5 es igual, como volumen, al cubo construido sobre una dimensión lineal proporcional a 6.
Margalit, que se presenta como doctor en Historia, sorprende en su libro con análisis de corte filósofico, especialmente los relativos al «poder» que acuñó en su día Michel Foucault, que aparecen de forma constante en numerosos fragmentos de la obra; por ejemplo, cuando señala que los esfuerzos de modernización exigidos por Israel, como tutor de la zona palestina de Jerusalén, son en realidad mecanismos de control, de poder: «Cuando el municipio exigió a los locales de las carnicerías de Jerusalén Oriental modernizar sus instalaciones a fin de mantener la mercancía con la refrigeración adecuada, al igual que lo estipulado en Israel, dicha medida podría ser percibida como una intervención legítima de salubridad pública, pero también, y no es menos cierto, como otra de las tantas medidas de intromisión destinadas a “israelizar” la parte oriental de la ciudad e intensificar el control israelí. Cuando Israel exige al servicio de transporte público renovar la flota de vehículos, y obliga a los conductores a realizar cursos de seguridad vial, está mejorando el servicio público, pero, a la vez, mandando tentáculos hacia diversas áreas de la actividad pública. Probablemente se trata de dos caras de una misma moneda. Más aún, medidas claramente opresoras pueden, en circunstancias determinadas, acarrear efectos positivos: la expropiación de tierras con el fin de construir una clínica, un colegio o pavimentar caminos será una medida justificada, a pesar de que toda confiscación de propiedades efectuada por la fuerza ocupante es, por definición, un acto de coerción» (38-9).
Los griegos pensaban que la geometría describía el espacio real en el que vivimos, y suponían que el espacio físico tenía que ser euclidiano. La pregunta matemática «¿puede existir un espacio tetradimensional en un sentido conceptual?» se confundía con la pregunta física «¿puede existir un espacio real con cuatro dimensiones?». […]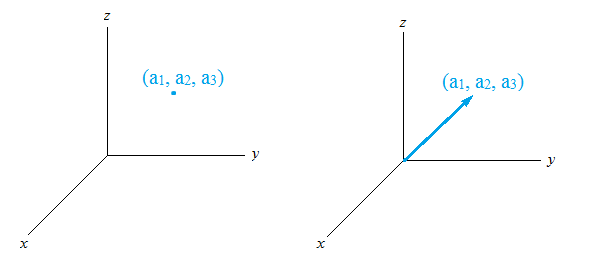
La ideología es mi pastor, nada me falta, exclama el izquierdista y eso le ahorra pensar, leer y estudiar y argumentar. Está iluminado con la fe del carbonero. Por eso los izquierdistas son fanáticos y establecen una suspensión teleológica de la ética convirtiendo la enemistad política en enemistad personal. Son como los luteranos: la fe sola les basta y les salva. Sola fides… Las obras no son necesarias. Es así como se manifiesta esta fe política fanática y maniquea. Como consideran que la sociedad burguesa no sirve y que sus instituciones, lenguaje, instituciones, moral, ética son superestructuras, pues no tienen inconveniente en utilizar los fines que sean convenientes para la revolución y para destruir el orden social con los costes humanos y materiales consiguientes, considerando que la historia los perdonará y que el bienestar de las generaciones futuras lo justifica y redime todo.
A modo de ilustración, podemos dar unas pinceladas sobre las esencias térmicas: el género generador de estas lo constituyen, a juicio del autor, aquellos «medios que los grupos de homínidos utilizan para controlar su temperatura y poder sobrevivir a los cambios drásticos de clima» —desde las pieles hasta las hogueras— y su diferencia específica radica en el control de la producción artificial del fuego. Partiendo de esto, el núcleo podrá ser situado en los hornos, que serán una introducción del fuego controlado, gracias a diversos aislantes, en el hogar y, además, coincidirán con «con la aparición de la producción en masa y el comercio manufacturado, la escritura en tablillas cocidas y sobre todo la extensión de las primeras ciudades con los imperios absolutos. En lo que respecta al cuerpo de esta esencia, Martín Jiménez no especificará qué atributos son propios de cada especie del curso, sino que tan solo sugerirá que «comprende una infinidad de tipos de hornos. Se trata de sistemas artificiales que caen bajo la primera y segunda ley de la termodinámica». En general, el autor no concederá mucha importancia al cuerpo de ninguna de las esencias técnicas que analiza —a diferencia de lo que hacía el propio Bueno—, sino que yuxtapondrá la distinción tecnológico/nematológico a la teoría de esencia, centrándose en las fantasiosas construcciones ideológicas, como veremos a continuación, que brotan de las prácticas técnicas.
Revista Metábasis 